방

The CoordConv layer ROS Gazebo에서 DART physics engine을 적용하는 방법 참고 Parameters Applicable to All Physics Engines Creating a Custom World File ROS integration overview Physics Parameters SDFormat - Physics   아직 완벽하게 적용하진 못 하여 roslaunch 를 실행시켰을 때 터미널에 오류가 나긴 하지만('문제점' 참고) 어쨌든 DART가 적용되어 내가 시도했던 방법을 기록해 보았다.   CMakeLists.txt 파일 수정 ROS integration overview 에서 CMakeLists.txt 부분을 참고하여 내가 생성했던 패키지 CMakeLists.txt 에서 빠진 부분을 추가했다.(ROS 패키지 생성은 여기 를 참고했다.) 다만, 링크에 있는 것들을 다 넣어주었을 때는 catkin_make 실행 씨 빌드가 안 되는 오류가 발생했다. 아래 부분을 제외하고 반영했더니 catkin_make 가 제대로 실행되었다. # Depend on system install of Gazebo find_package(ga

The CoordConv layer CoordConv 에 대한 방법론 간단 정리 참고 논문 (원문) An intriguing failing of convolutional neural networks and the CoordConv solution 블로그 설명 https://pajamacoder.tistory.com/13   블로그 설명을 보고 CoordConv layer 방법의 대략적인 감을 잡아보았다. 구현을 위해 논문의 관련 section을 읽고 그 내용을 정리 해 보았다. ( 3 The CoordConv layer 부분만 읽고 해당 내용 정리) Figure 3: Comparison of 2D convolutional and CoordConv layers. (left) A standard convolutional layer maps from a representation block with shape $h \times w \times c$ to a new representation of shape $h' \times w' \times c'$. (right) A CoordConv layer has the same functional signature, but accomplishes the mapping by first concatenating extra channels to the incoming representation. These channels contain hard-coded coordinates, the most basic version of which

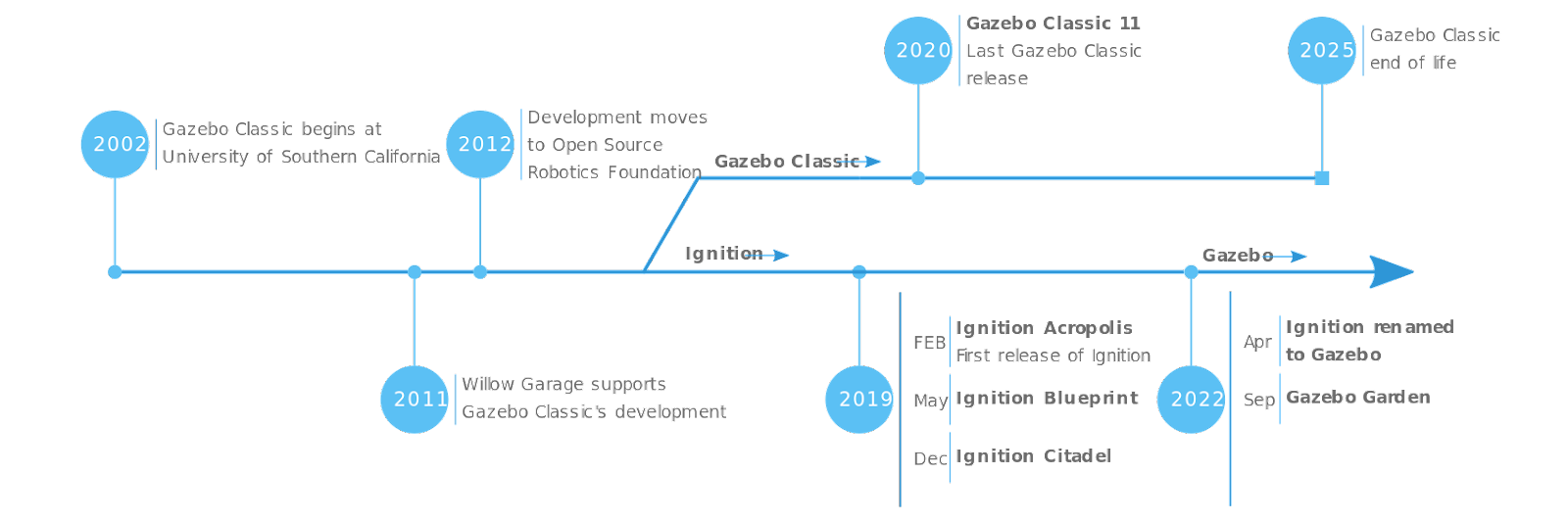
Gazebo Gazebo 사용에 대한 내용 정리  2022년 7월, 연구실에서 진행하는 과제를 통해 Gazebo를 사용해보기 시작했다. 설치부터 시뮬레이션 사용까지 알아두면 좋을 내용들을 적어 두려고 한다.  Gazebo를 설치하려고 보니 https://gazebosim.org/home 와 https://classic.gazebosim.org/ 두 개의 페이지가 존재했다. 어떤 것을 참고해서 설치 해야 할지 헷갈렸었는데 about 페이지에 설명을 보고 어떤 차이가 있는지 알 수 있었다. (아마도 2019년) Gazebo Classic과 Gazebo로 두 개의 branch로 나뉘어 개발이 진행되었고, Gazebo Classic은 2025년까지 지원해준다고 한다. History 설명을 읽어보니 브랜치를 나누면서 Ignition이라는 이름으로 바꿨는데 상표권 문제로 인해 다시 Gazebo로 바꿨다고 한다.  Gazebo에서 Dart 물리엔진을 사용하기 위해 이번에 새로 설치하게 되었는데, 나의 경우 향후 지원을 고려하여 'Gazebo'를 사용하고자 한다. 설치할 때 아래 설명 중, 반드시 main documentation에 들어가서 Releases를 확인하도록 하자! 2022. 07. 27. 현재 기준 Fortress가 recommended version이고 Garden은 아직 개발 중인 버전인데 제대로 확인 안 하고 the latest installation tutorial here에 들어갔더니 Garden 설치에 대한 안내가 되어있어서 고생만 하고 제대로 설치하지 못 했다. Recommened version에 들어가서 Binary installation을 통해 설치 해 주도록 하자. 나 같은 경우

Ubuntu_seting_nomodeset Ubuntu 18.04 설치 중 or 설치 후 부팅이 제대로 되지 않는 오류 발생   최근 새로운 workstation에 Ubuntu 18.04를 설치를 하다가 두 가지 문제가 발생했다. 설치 직후, 부팅할 때 화면이 깨짐 부팅디스크 인식 후, 메뉴로 들어갈 때 GUI를 보는 단계에서 화면 깨짐 두 가지 모두 Install Ubuntu 또는 Trying Ubuntu without install 이 나오는 화면깨짐 현상이 발생했다. Alt + F2를 누르면 아래와 같은 오류가 창에 뜬다. nouveau 0000:01:00.0: DRM: failed to create kernel channel, -22  원인은 컴퓨터에 있는 그래픽 드라이버가 제대로 인식되지 않는 탓이라고 한다. (사실 나도 잘 아는 부분이 아니라 자세한 설명은 생략...)   해결 방법 Install Ubuntu 또는 Trying Ubuntu without install 와 같은 부팅 디스크의 메뉴가 뜨는 창에서 키보든 e 를 누른다. 텍스트 편집 창에서 quiet splash ---- 부분에서 ---- 를 nomodeset 으로 바꿔준다.

Multiplicity of NURBS B-Spline Surface B-Spline Surface를 공부했던 내용을 간단 정리  Spline Curve 자료와 마찬가지로 SNU open courseware에서 이규열 교수님의 ' Computer-Aided Ship Design ' 수업자료를 참고하여 알아보았다.  Spline surface또한 curve와 마찬가지로 Bezier Surface가 있고 이를 일반화한 B-spline Surface가 있다. 전반적으로 보았을 때, Surface를 표현하는 것은 (u,v)벡터 방향의 두 orthogonal curve를 이용하여 표현한다. Surface를 표현하는 방식 중 'Tensor product approach'가 있는데 Fig. 1 처럼 파란 색으로 나타낸 moving curve가 붉은 색 directional curve를 따라 움직이면서 그리는 자취를 방식을 말한다. 본 글에서는 Bezier Surface가 어떤 방식으로 그려지는지 다룬다. Bezier Surface  $3 \times 3$ points $b_{ij}$가 있다고 했을 때,  (1) start/end moving curve를 생성 (파란색 실선) $$ \mathbf{b}_S(u)= \mathbf{b}_{00}B^2_0(u) + \mathbf{b}_{10}B^2_1(u) + \mathbf{b}_{20}B^2_2(u) $$ $$ \mathbf{b}_E(u)= \mathbf{b}_{02}B^2_0(u) + \mathbf{b}_{12}B^2_1(u) + \mathbf{b

Knot Multiplicity at B-spline curve What is knot multiplicity exactly? In the STEP file, the knot muliplicity value from the second value to the second to last value may not be '1'. However, there was only '1' in the study material of SNU open courseware. B-Spline says "A curve is p-k times differentiable at a point where k duplicate knot values occur. The knot values determine the extent of the control of the control points.". I understand the 'knot muliplicity' by control range of control points. Full-multiplicity knot helps me to understand vague meaning of controlling knot value.  As a result, I couldn't exactly understand the 'knot muliplicity', but I just understood roughly what it meant.