CoordConv 방법론 부분 간단 정리

CoordConv 에 대한 방법론 간단 정리

참고
• 논문 (원문) An intriguing failing of convolutional neural networks and the CoordConv solution
• 블로그 설명 https://pajamacoder.tistory.com/13

  블로그 설명을 보고 CoordConv layer 방법의 대략적인 감을 잡아보았다. 구현을 위해 논문의 관련 section을 읽고 그 내용을 정리 해 보았다.
(3 The CoordConv layer 부분만 읽고 해당 내용 정리)

Figure 3: Comparison of 2D convolutional and CoordConv layers. (left) A standard convolutional layer maps from a representation block with shape $h \times w \times c$ to a new representation of shape $h' \times w' \times c'$. (right) A CoordConv layer has the same functional signature, but accomplishes the mapping by first concatenating extra channels to the incoming representation. These channels contain hard-coded coordinates, the most basic version of which is one channel for the $i$ coordinate and one for the $j$ coordinate, as shown above. Other derived coordinates may be input as well, like the radius coordinate used in ImageNet experiments (Section 5).

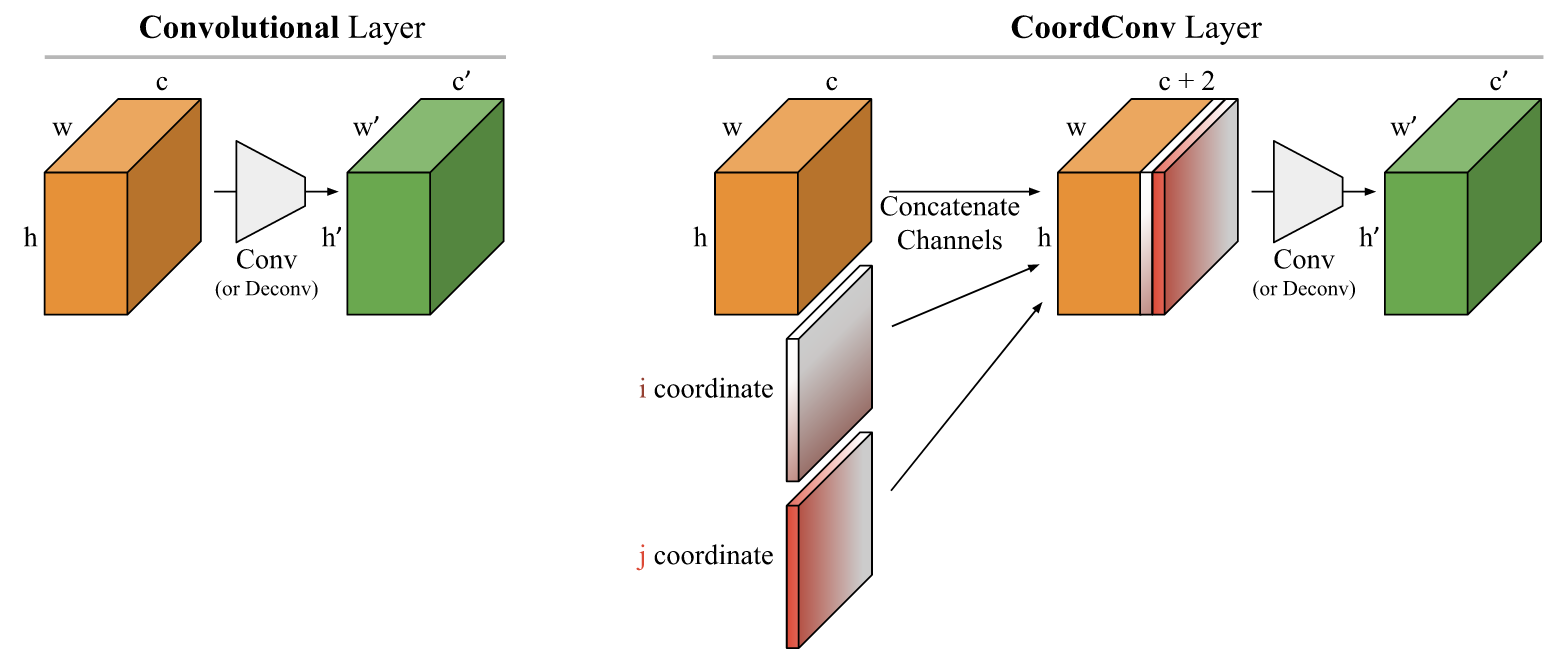
(이하 논문 본문을 읽고 이해한 내용)
  Figure 3의 오른쪽 'CoordConv layer'를 보면 i coordinate은 위에서 아래로 그라데이션이 있고 j coordinate은 왼쪽에서 오른쪽으로 그라데이션이 있다. 이는 기존 convolutional layer와 차이점을 그림으로 묘사한 것이다. 기존 channel에 더해지는 i, j coordinate matrix는 크기가 $h \times w$ 이고 rank-1 matrix이다. i coordinate에서 각각의 행들은 같은 값을 갖고, j coordinate에서 각각의 열들은 같은 값을 갖는다. 예를들면 i coordinate의 1번 행은 0들로 채워지고 2번 행은 1들고 채워지고 3번 행은 2들로 채워지는 식이다. j coordinate의 열들도 마찬가지 방식으로 채워진다. 저자들은 모든 실험에서 두 i, j coordinate 값들을 $[-1, 1]$ 범위 안에 linear scaling 했다. 어떤 실험의 경우엔 3번 째 채널로 $r = \sqrt{(i-h/2)^2+(j-w/2)^2}$의 형태로 $r$ coordinate을 추가했다.

Number of parameters.       Bias parameters를 무시했을 때, square kernel size k인 일반적인 convolutional layer는 $cc'k^2$ 만큼의 weight들을 갖게 된다. 반면에 동일한 CoordConv layer는 $(c + d)c'k^2$만큼의 weight들을 갖는다. 여기서 d는 coordinate dimensions (2 또는 3)이다. Parameter들의 증가 정도는 input channel의 원래 크기에 따라 달라진다. ($d$ 대비 $c$가 어느정도 인지에 따라 증가율이 다르다는 뜻)