Spline Surface
B-Spline Surface를 공부했던 내용을 간단 정리
Spline Curve 자료와 마찬가지로 SNU open courseware에서 이규열 교수님의 'Computer-Aided Ship Design' 수업자료를 참고하여 알아보았다.
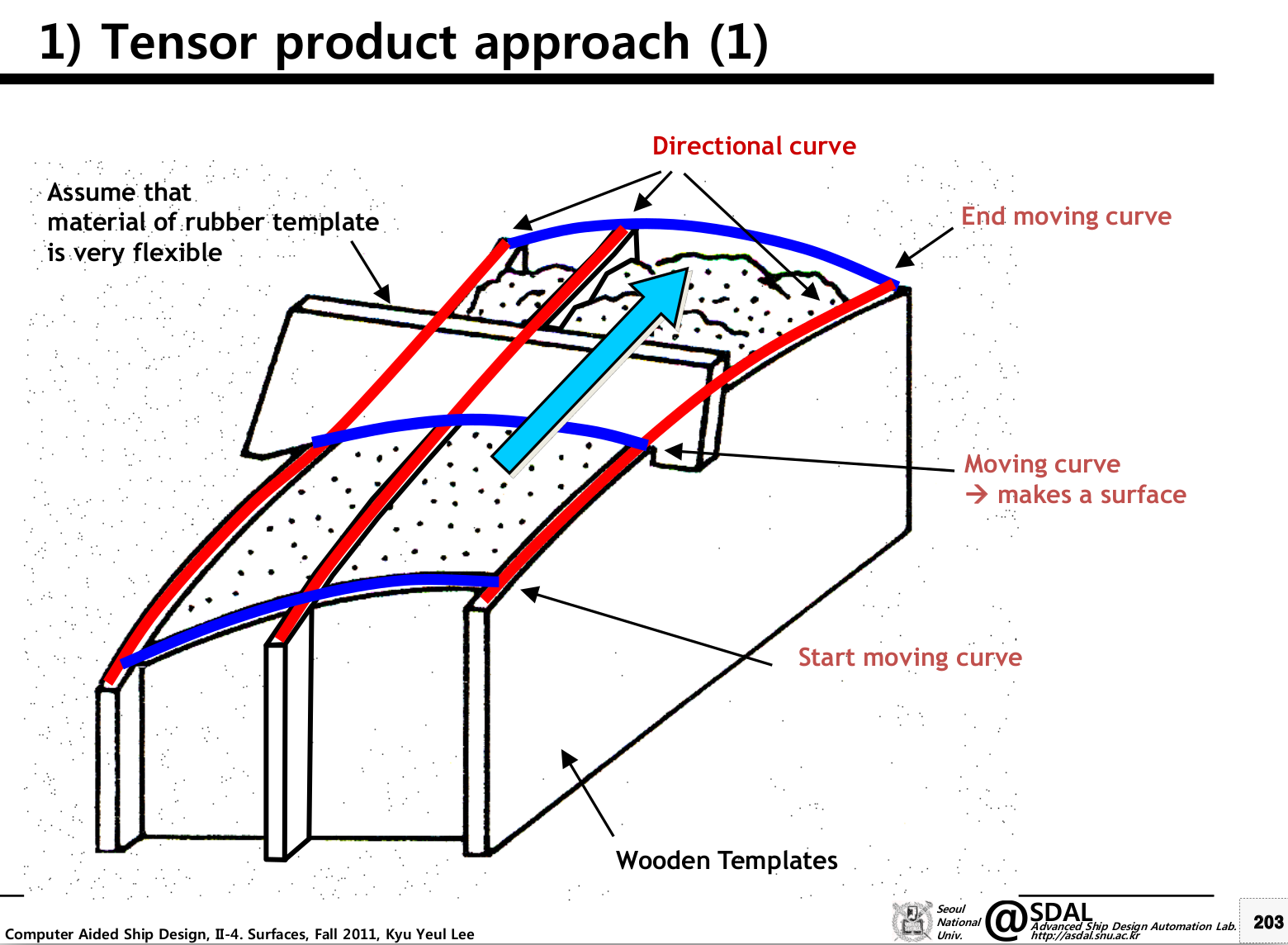
Spline surface또한 curve와 마찬가지로 Bezier Surface가 있고 이를 일반화한 B-spline Surface가 있다. 전반적으로 보았을 때, Surface를 표현하는 것은 (u,v)벡터 방향의 두 orthogonal curve를 이용하여 표현한다. Surface를 표현하는 방식 중 'Tensor product approach'가 있는데 Fig. 1 처럼 파란 색으로 나타낸 moving curve가 붉은 색 directional curve를 따라 움직이면서 그리는 자취를 방식을 말한다. 본 글에서는 Bezier Surface가 어떤 방식으로 그려지는지 다룬다.
Spline surface또한 curve와 마찬가지로 Bezier Surface가 있고 이를 일반화한 B-spline Surface가 있다. 전반적으로 보았을 때, Surface를 표현하는 것은 (u,v)벡터 방향의 두 orthogonal curve를 이용하여 표현한다. Surface를 표현하는 방식 중 'Tensor product approach'가 있는데 Fig. 1 처럼 파란 색으로 나타낸 moving curve가 붉은 색 directional curve를 따라 움직이면서 그리는 자취를 방식을 말한다. 본 글에서는 Bezier Surface가 어떤 방식으로 그려지는지 다룬다.
Bezier Surface
$3 \times 3$ points $b_{ij}$가 있다고 했을 때,
(1) start/end moving curve를 생성 (파란색 실선)
$$ \mathbf{b}_S(u)= \mathbf{b}_{00}B^2_0(u) + \mathbf{b}_{10}B^2_1(u) + \mathbf{b}_{20}B^2_2(u) $$ $$ \mathbf{b}_E(u)= \mathbf{b}_{02}B^2_0(u) + \mathbf{b}_{12}B^2_1(u) + \mathbf{b}_{22}B^2_2(u) $$ (2) directional curve를 생성 (붉은색 실선)
$$ \mathbf{b}_0(u)= \mathbf{b}_{00}B^2_0(u) + \mathbf{b}_{01}B^2_1(u) + \mathbf{b}_{02}B^2_2(u) $$ $$ \mathbf{b}_1(u)= \mathbf{b}_{10}B^2_0(u) + \mathbf{b}_{11}B^2_1(u) + \mathbf{b}_{12}B^2_2(u) $$ $$ \mathbf{b}_2(u)= \mathbf{b}_{20}B^2_0(u) + \mathbf{b}_{21}B^2_1(u) + \mathbf{b}_{22}B^2_2(u) $$ 와 같이 나타낼 수 있다.
(2)를 matrix form으로 나타내면 $$ \begin{bmatrix} \mathbf{b}_0(u) \cr \mathbf{b}_1(u) \cr \mathbf{b}_2(u) \end{bmatrix} = \begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix} \begin{bmatrix} B^2_0(u) \cr B^2_1(u) \cr B^2_2(u) \end{bmatrix} $$ 와 같은 형태로 나타낼 수 있고, 여기서 나온 $\mathbf{b}_i$벡터를 사용하여 $\mathbf{b}(u,v)$ 벡터를 표현할 수 있다. $$ \eqalign{ \mathbf{b}(u,v) &= \mathbf{b}_{0}(v)B^2_0(u) + \mathbf{b}_{1}(v)B^2_1(u) + \mathbf{b}_{2}(v)B^2_2(u) \\ &= \begin{bmatrix} B^2_0(u) & B^2_1(u) & B^2_2(u) \end{bmatrix} \begin{bmatrix} \mathbf{b}_{0}(v) \cr \mathbf{b}_{1}(v) \cr \mathbf{b}_{2}(v) \end{bmatrix} } $$ 따라서, 최종적으로 아래와 같은 surface를 표현하는 식을 얻을 수 있다. $$ \eqalign{ \mathbf{b}(u,v) &= \begin{bmatrix}B^2_0(u) & B^2_1(u) & B^2_2(u)\end{bmatrix} \begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix} \begin{bmatrix} B^2_0(u) \cr B^2_1(u) \cr B^2_2(u) \end{bmatrix} \\ &= \sum_{j=0}^2\sum_{i=0}^2 \mathbf{b}_{ij}B_i^2(u)B_j^2(v) } $$ 위에서 $\begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix}$ 는 Bezier surface의 control point들이다.
(1) start/end moving curve를 생성 (파란색 실선)
$$ \mathbf{b}_S(u)= \mathbf{b}_{00}B^2_0(u) + \mathbf{b}_{10}B^2_1(u) + \mathbf{b}_{20}B^2_2(u) $$ $$ \mathbf{b}_E(u)= \mathbf{b}_{02}B^2_0(u) + \mathbf{b}_{12}B^2_1(u) + \mathbf{b}_{22}B^2_2(u) $$ (2) directional curve를 생성 (붉은색 실선)
$$ \mathbf{b}_0(u)= \mathbf{b}_{00}B^2_0(u) + \mathbf{b}_{01}B^2_1(u) + \mathbf{b}_{02}B^2_2(u) $$ $$ \mathbf{b}_1(u)= \mathbf{b}_{10}B^2_0(u) + \mathbf{b}_{11}B^2_1(u) + \mathbf{b}_{12}B^2_2(u) $$ $$ \mathbf{b}_2(u)= \mathbf{b}_{20}B^2_0(u) + \mathbf{b}_{21}B^2_1(u) + \mathbf{b}_{22}B^2_2(u) $$ 와 같이 나타낼 수 있다.
(2)를 matrix form으로 나타내면 $$ \begin{bmatrix} \mathbf{b}_0(u) \cr \mathbf{b}_1(u) \cr \mathbf{b}_2(u) \end{bmatrix} = \begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix} \begin{bmatrix} B^2_0(u) \cr B^2_1(u) \cr B^2_2(u) \end{bmatrix} $$ 와 같은 형태로 나타낼 수 있고, 여기서 나온 $\mathbf{b}_i$벡터를 사용하여 $\mathbf{b}(u,v)$ 벡터를 표현할 수 있다. $$ \eqalign{ \mathbf{b}(u,v) &= \mathbf{b}_{0}(v)B^2_0(u) + \mathbf{b}_{1}(v)B^2_1(u) + \mathbf{b}_{2}(v)B^2_2(u) \\ &= \begin{bmatrix} B^2_0(u) & B^2_1(u) & B^2_2(u) \end{bmatrix} \begin{bmatrix} \mathbf{b}_{0}(v) \cr \mathbf{b}_{1}(v) \cr \mathbf{b}_{2}(v) \end{bmatrix} } $$ 따라서, 최종적으로 아래와 같은 surface를 표현하는 식을 얻을 수 있다. $$ \eqalign{ \mathbf{b}(u,v) &= \begin{bmatrix}B^2_0(u) & B^2_1(u) & B^2_2(u)\end{bmatrix} \begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix} \begin{bmatrix} B^2_0(u) \cr B^2_1(u) \cr B^2_2(u) \end{bmatrix} \\ &= \sum_{j=0}^2\sum_{i=0}^2 \mathbf{b}_{ij}B_i^2(u)B_j^2(v) } $$ 위에서 $\begin{bmatrix} \mathbf{b}_{00} & \mathbf{b}_{01} & \mathbf{b}_{02} \cr \mathbf{b}_{10} & \mathbf{b}_{11} & \mathbf{b}_{12} \cr \mathbf{b}_{20} & \mathbf{b}_{21} & \mathbf{b}_{22} \end{bmatrix}$ 는 Bezier surface의 control point들이다.
B-Spline Surface
B-spline Surface는 행렬 및 벡터의 크기가 바뀔 수 있고 knot가 추가될 뿐, 전반적으로 Bezier Surface와 비슷하다. 자세한 내용은 SNU의 수업자료 211쪽을 참고하도록 하자.

댓글
댓글 쓰기