Frenet-Serret formulas (프레네-세레 공식)
The tangent, normal, and binormal unit vectors, often called T, N, and B, or collectively the Frenet–Serret frame or TNB frame, together form an orthonormal basis spanning ℝ3 and are defined as follows:
- T is the unit vector tangent to the curve, pointing in the direction of motion.
- N is the normal unit vector, the derivative of T with respect to the arclength parameter of the curve, divided by its length.
- B is the binormal unit vector, the cross product of T and N.
The Frenet–Serret formulas are:
where d/ds is the derivative with respect to arclength, κ is the curvature, and τ is the torsion of the curve. The two scalars κ and τ effectively define the curvature and torsion of a space curve. The associated collection, T, N, B, κ, and τ, is called the Frenet–Serret apparatus. Intuitively, curvature measures the failure of a curve to be a straight line, while torsion measures the failure of a curve to be planar.
Definitions[edit]
Let r(t) be a curve in Euclidean space, representing the position vector of the particle as a function of time. The Frenet–Serret formulas apply to curves which are non-degenerate, which roughly means that they have nonzerocurvature. More formally, in this situation the velocity vector r′(t) and the acceleration vector r′′(t) are required not to be proportional.
Let s(t) represent the arc length which the particle has moved along the curve. The quantity s is used to give the curve traced out by the trajectory of the particle a natural parametrization by arc length, since many different particle paths may trace out the same geometrical curve by traversing it at different rates. In detail, s is given by
Moreover, since we have assumed that r′ ≠ 0, it follows that s(t) is a strictly monotonically increasing function. Therefore, it is possible to solve for t as a function of s, and thus to write r(s) = r(t(s)). The curve is thus parametrized in a preferred manner by its arc length.
With a non-degenerate curve r(s), parameterized by its arc length, it is now possible to define the Frenet–Serret frame (or TNB frame):
- The tangent unit vector T is defined as
- The normal unit vector N is defined as
- The binormal unit vector B is defined as the cross product of T and N:
From equation (2) it follows, since T always has unit magnitude, that N is always perpendicular to T. From equation (3) it follows that B is always perpendicular to both T and N. Thus, the three unit vectors T, N, and B are all perpendicular to each other.
The Frenet–Serret formulas are:
The Frenet–Serret formulas are also known as Frenet–Serret theorem, and can be stated more concisely using matrix notation:[1]
This matrix is skew-symmetric.
reference : https://en.wikipedia.org/wiki/Frenet%E2%80%93Serret_formulas
Question:
위의 공식들이 어떻게 유도되고 왜 저런 관계가 이루어지는지 정확히 이해가 잘 안가는데 아시는 분은 답글에 설명 혹은 참고할만한 URL부탁드립니다.
I don't understand exactly how the above formulas derived and why such relationships achieved. Please reply about above formulas or let me know URL that can I refer to.
Question:
위의 공식들이 어떻게 유도되고 왜 저런 관계가 이루어지는지 정확히 이해가 잘 안가는데 아시는 분은 답글에 설명 혹은 참고할만한 URL부탁드립니다.
I don't understand exactly how the above formulas derived and why such relationships achieved. Please reply about above formulas or let me know URL that can I refer to.


 will be in the direction N and the curvature describes the speed of rotation of the frame.
will be in the direction N and the curvature describes the speed of rotation of the frame.


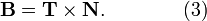


 is the
is the  is the
is the 
댓글
댓글 쓰기